As I have not yet studied advanced theoretical computer science courses in subjects like type theory, logic, abstract algebra, category theory, and so on.
I have recently been trying to learn the basics on my own.
Previous research attempts has time and time again led me back to the fundamentals of rewriting systems,1
and I have decided to take a deeper dive into the basics to prepare myself for more advanced topics in the future.
❗ Disclaimer#
I am not an expert in the field in any way, this article is merely a collection of my notes and thoughts on the subject, and exists to help me understand the topic of rewriting systems better. This work will in no way be exhaustive, but rather a short personal exploration and self-study.
I will be using various resources, including books, papers and online articles to help me understand the topic better, and I hope you find this article helpful in your own learning journey as well. A great book I have found on the subject is Term Rewriting and All That by Franz Baader and Tobias Nipkow.2 I will use the terms abstract rewriting systems, or abstract reduction systems (ARS) and rewriting systems interchangeably,342 as I am not focusing on any specific type of rewriting system (Frankly, I am not sure if there is a difference between the two).
What are Rewriting Systems?#
A rewriting system is a formal system that consists of a set of rules that describe how to rewrite terms and are a fundamental concept in computer science, mathematics, and logic.513 They are used to model a wide range of computational processes and reasoning in for example lambda calculus.6 Rewriting systems are used in many areas of computer science, including programming languages, compilers, and automated theorem proving.
An abstract rewriting system (ARS) consists of a set of elements \( A \), the set of terms \(T\)7 made up from elements, and binary relations \(R\)8 on terms7 (rewrite rules). The set of symbolic terms can sometimes be a combination of elements (\(A \subseteq T\)), indeterminate variable symbols (\(V \subseteq T\)), operator symbols (\(O \subseteq T\)), etc. This depends on the model domain of the system. A relation between two terms is denoted by \( \rarr \) and is called the reduction, rewrite relation or rule.318 Though the relation is not actually performing any “reducing” action or computation, it is merely a description of how one term can be rewritten into another term. The system is thus defined by a set of rules that describe how terms can be rewritten (transformed), and these rules are applied to terms to produce new terms. Formally, \( (A, R) \) is an ARS where \( A \) is a set of elements and \( R \) is a set of rewrite relations from one term to another \( R \subseteq A \times A \). Again, where terms \( t \in T \) are made up of elements \( A \), like \( t ::= A \mid \ldots \), and potentially more constructs depending on domain (shown by \( \ldots \)).
Alternative notations for rewriting systems might use \( (A, \rarr) \) where \( \rarr \) denotes the rewrite relation set. Others might use multiple relation sets to define a system, denoted as \( (A, \rarr_1, \rarr_2, \ldots, \rarr_n) \), which together define the relation set \( R = \rarr_1 \cup \rarr_2 \cup \ldots \cup \rarr_n \) in \( (A, R) \).
Example (A, B, C)#
Consider the following rewriting system with the set of ground and linear9 elements \( \lbrace a, b, c \rbrace \) and the rules:
$$ \begin{align*} a & \rarr b \\ b & \rarr c \\ \end{align*} $$
The system can be represented as a directed graph where the nodes are the elements and the edges are the rules. The graph is shown below:
In this system, the element and term \( a \) can be rewritten to \( b \) and \( b \) can be rewritten to \( c \). The term \( a \) can be rewritten to \( c \) by applying the rules \( a \rarr b \) and \( b \rarr c \) in sequence. This is an example of a simple rewriting system.
Example (Logic)#
Let’s consider a more complex example, a rewriting system that models logic5 and basics of boolean algebra.10 The set of elements is \( \lbrace \top, \bot \rbrace \) where \( \top \) represents true and \( \bot \) represents false. A Term \( t \) can be made up of literal elements and propositional variables11 \( p, q, r, \ldots \in V \), formalized as \( t ::= \top \mid \bot \mid V \mid \lnot t \mid t \land t \mid t \lor t \). The rules1 represent logical axioms,5 logical equivalences12 and boolean algebra identities,10 defined as:
$$ \begin{align*} \lnot \lnot p &\rarr p \\ p \land q &\rarr q \land p \\ p \lor q &\rarr q \lor p \\ \lnot (p \land q) &\rarr \lnot p \lor \lnot q \\ \lnot (p \lor q) &\rarr \lnot p \land \lnot q \\ p \land (q \land r) &\rarr (p \land q) \land r \\ p \lor (q \lor r) &\rarr (p \lor q) \lor r \\ (p \land q) \lor r &\rarr (p \lor r) \land (q \lor r) \\ \\ p \land \top &\rarr p \\ p \lor \bot &\rarr p \\ p \land \bot &\rarr \bot \\ p \lor \top &\rarr \top \\ p \land \neg p &\rarr \bot \\ p \lor \neg p &\rarr \top \\ \end{align*} $$
These rewrite relations often have a more complex term on the left-hand side and a simpler term on the right-hand side. This is a common pattern and hints at the normalization13 properties of the system, discussed in the next section. Using this system we can write any expression in its conjunctive normal form (CNF) or disjunctive normal form (DNF) by applying the rules in sequence.14
Below is an example of how the rewrite system can be used to simplify a logical formula: \( \lnot((p \land q) \lor \lnot q)\) to \(\lnot(p \land q) \).
This system models logical reasoning and can be used to prove theorems and derive new logical formulas, and is an example of how rewriting systems can be used in practice.
More Notation#
Before reading any academic papers using rewriting systems, we’ll need to understand some extended denotation used to describe the rules and properties of rewriting systems. Note, I’m trying to be as comprehensive as possible, but there are lots of different notations used in the literature. Also, I’m not an expert, so take this with a grain of salt.
Direct Reduction#
Denotations include: \( R \), \( \xrightarrow{} \) and \( \rarr \).
A regular relation that represents a single step in a rewriting process where one term is directly transformed into another based on a specific rewrite rule.
What are Closures?#
Before we go into detail on the different type of notations, let’s first understand what closures are in the context of rewriting systems. It’s easy to get confused with the term, as it may have a different meaning in other subjects.
Mathematical definition#
A subset of a given set is closed under an operation of the larger set if performing that operation on members of the subset always produces a member of that subset. For example, the natural numbers are closed under addition, but not under subtraction: \(1 − 2\) is not a natural number, although both \(1\) and \(2\) are. Similarly, a subset is said to be closed under a collection of operations if it is closed under each of the operations individually. The closure of a subset is the result of a closure operator applied to the subset. The closure of a subset under some operations is the smallest superset that is closed under these operations. It is often called the span (for example linear span) or the generated set.15
I interpret this as a closure being a set of elements that when some operation is applied to them, the result is always a member of the same set. Thus the operation is closed under the set of elements, meaning no elements are lost or gained after the operation, coming from any other set elsewhere, somehow.
The classical example here is of course the natural numbers being closed under addition but not under subtraction. Because adding two natural numbers always results in another natural number, and subtracting two natural numbers may result in a negative number, which is not a natural number.
$$ \begin{align*} & \forall a, b \in \mathbb{N} \iff a + b \in \mathbb{N} \hspace{1cm} \text{OK} & \\ & \not \forall a, b \in \mathbb{N} \not \Rarr a - b \in \mathbb{N} \hspace{1cm} \text{Not OK} & \\ \end{align*} $$
So, what does this mean in the context of rewriting systems? Simply put, a closure-relation is just like a regular relation, but with additional properties.15 This is done by extending a basic relation \( R \) or \( \rarr \) to expand the set of allowable transformations between terms. Closures are fundamental in understanding how terms can evolve in a system beyond simple direct transformations, incorporating sequences, reversals, and self-referential transformations, among others.
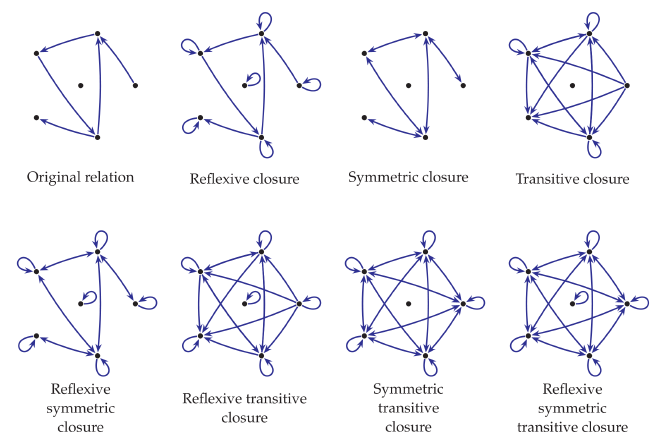
Above is a diagram showing the different types of closures of a relation.
Transitive Closure#
Denotations include: \( \xrightarrow{+} \) and \( \rarr^+ \).
The first closure we’ll look at is the transitive closure of a relation.
Mathematical definition#
A binary relation \(R\) on a set \(X\) is transitive if, for all elements \(a, b, c \in X\), whenever \(R\) relates \(a\) to \(b\) and \(b\) to \(c\), then \(R\) also relates \(a\) to \(c\).
The transitive closure of a relation extends the original relation \( \rarr \) so that it includes direct and sequences of transformations between terms. For example, if term \( a \rarr b \) and term \( b \rarr c \), then in the transitive closure, term \( a \) is considered to directly reach term \( c \), notated \( a \rarr^+ c \). The example below generalize to any number of intermediate terms \( b_1, b_2, \ldots, b_N \).
Simply put, \( a \rarr^+ c \) means that there is some sequence of rewrites transforming the term \( a \) to \( c \) (including one or more rewrites). This is the smallest relation that contains the original relation \( \rarr \) and is the transitive property of terms.1617
Reflexive Transitive Closure#
Denotations include: \( \xrightarrow{*} \) and \( \rarr^* \).
A reflexive relation \( R^* \) is a relation where every element in \(A\) is related to itself. This can be formally defined as:18
$$ \begin{align*} & \text{Relation } R \text{ is reflexive } \iff & \forall x \in A, & \ x R x \\ & & \text{or} \hspace{4mm} & \ x \rarr x \\ & & \text{or} \hspace{4mm} & \ (x, x) \in R \end{align*} $$
As every intersection of reflexive relations is reflexive, this defines a closure. A reflexive-transitive closure is a closing relation that is both reflexive and transitive.191617 That is having the properties of both the transitive and reflexive closures, meaning that it includes direct, sequence and self-referential transformations between terms.
Symmetric Closure#
Denotations include: \( \xleftrightarrow{} \) and \( \lrarr \).
This is a relation that is symmetric if, for all elements \(a, b \in X\), whenever \(R\) relates \(a\) to \(b\), then \(R\) also relates \(b\) to \(a\). This is a closure that includes bi-directional transformations between terms. Formally, a relation \( R \) is symmetric if \( a \rarr b \implies b \rarr a \), where \( \lrarr \ = (\rarr \cup \rarr^{-1}) \) and \( \rarr^{-1} \ = \lbrace (b, a) \mid (a, b) \in \rarr \rbrace \).38
Formally a symmetric closure \( S \) of a relation \( R \) on the set of elements \( A \) is defined as:
$$ \begin{align*} S = R \cup R^{-1} \hspace{2mm} \text{where} \hspace{2mm} R^{-1} = \lbrace a, b \in A \mid (b, a) \in R \rbrace \end{align*} $$
Reflexive Transitive Symmetric Closure#
Denotations include: \( \xleftrightarrow{*} \), \( \lrarr^* \) and \( \sim \).
This is a relation that is both reflexive, transitive and symmetric. That is having the properties of the transitive and reflexive closures, and the symmetric property, meaning that it includes direct, sequence, self-referential and bi-directional transformations between terms.1816171920
Similarly, the reflexive transitive symmetric closure or equivalence closure of a relation is the smallest equivalence relation.1521
For all \( a, b, c \in A \):21
- Reflexive: \( a \rarr^* a \).
- Transitive: \( a \rarr^* b \land b \rarr^* c \implies a \rarr^* c \).
- Symmetric: \( a \rarr^* b \implies b \rarr^* a \).
Joinability#
Denotation: \( \downarrow \).
A less formal term of normal forms are joinable terms, where two terms are joinable if they can be rewritten to the same term. \( x \downarrow y \) denotes that there exists a term \( z \in A \) such that \( x \rarr^* z \land y \rarr^* z \), alternatively written as \( x \xrightarrow{*} z \xleftarrow{*} y \).
Composition#
Denotation: \( \circ \).
Composition is a binary operation that combines two relations to form a new relation. For example, using the denotation of a reflexive transitive closure relations, \( \xrightarrow{*} \), the composition of two relations \( R^* \circ S^* \) is defined as \( \lbrace (a, c) \mid \exists b \in A, a \xrightarrow{*}_R b \land b \xrightarrow{*}_S c \rbrace \), and can be expressed by the operator \( \xrightarrow{*}_R \circ \xrightarrow{*}_S \).
Properties#
Some properties of abstract term rewriting systems are termination,2223 confluence,24 normalization,13 completion252 and equivalence.12 A confluent and terminating ARS is called convergent or canonical.1
Termination#
Termination describes whether a rewriting system has a finite number of rewrites for any term in the system. An ARS is said to be terminating if there is no infinite chain \( x_{0} \rightarrow x_{1} \rightarrow x_{2} \rightarrow \cdots \) of rewrites.26
$$ \begin{align*} & \text{ARS is terminating} \iff \forall x_i \in A \\ % & \text{there is no infinite chain of rewrites } x_{0} \rightarrow x_{1} \rightarrow x_{2} \rightarrow \cdots \\ & \nexists x_{0}, x_{1}, x_{2}, \ldots \text{ such that } x_{0} \rightarrow x_{1} \rightarrow x_{2} \rightarrow \cdots \\ \end{align*} $$
Confluence#
“Confluence describes which terms in such a system can be rewritten in more than one way, to yield the same result”.24 A rewriting system is said to be confluent if, for any terms \( t, s, u \) such that \( t \rarr^* s \land t \rarr^* u \), there exists a term \( v \) such that \( s \rarr^* v \land u \rarr^* v \).24 In a confluent system, the (TODO) relation is called the confluence relation.
Confluence is a property that implies that if a term can be rewritten in more than one way (leading to multiple possible outcomes), all these paths will eventually converge to a common rewrite outcome, regardless of the choices made during rewriting. Formally, denoting that any term \(a\) can reach any term \(b\) (and vice versa) through a sequence of forward and backward steps, is instrumental in analyzing confluence. If this closure holds between any two rewrite results of the same term, the system is confluent. The symmetric closure \( \xleftrightarrow{*} \) is used to define confluence.
An ARS possess the Church-Rosser property if and only if \( x \xleftrightarrow{*} y \) implies \( x \downarrow y \) for all terms \( x, y \) in the system.243
$$ \begin{align*} & \text{Church-Rosser property} \iff \\ & \forall x, y \in A, x \xleftrightarrow{*} y \implies x \downarrow y \\ \end{align*} $$
Convergence#
Convergence is a combination of confluence and termination. A rewriting system is convergent if it is both confluent and terminating. Convergence guarantees that every term can be rewritten to a unique normal form.
Consistency#
In the context of logic and type systems, consistency refers to the property that there are no terms that can be both proved and disproved within the system. For rewriting systems, particularly those representing logical proofs, consistency means that there is no term that can be rewritten to both a theorem and its negation.
Decidability#
A rewriting system has the property of decidability if there is an effective procedure (algorithm) to determine whether, for any two given terms, one term can be rewritten to the other. This property is important for automated reasoning systems where it’s necessary to know whether a certain state can be reached.
Completion#
A rewriting system is complete if it is both confluent and strongly normalizing. Completeness is often desired in theorem proving and formal verification since it ensures that every valid proof can be found through a systematic search of the rewriting system.
Equivalence#
The property of equivalence in rewriting systems refers to the scenario where different sequences of rewrites on a term or from a term lead to outcomes that can be considered equivalent under the rewriting rules. The reflexive transitive symmetric closure \( \xleftrightarrow{*} \) is the smallest equivalence relation containing the original rewrite relation \( \rarr \). This closure indicates that any two terms related by this closure can be transformed into each other through a series of rewriting steps, forward or backward, indicating that they are equivalent in the context of the rewriting system.
Normal Forms#
A term in normal form13 (NF) is an irreducible, canonical representation of a term in a rewriting system. That is, no rewrite rules can be applied to the term to produce a new term. Formally, if \( (A, \rarr) \) is an ARS, a term \( t \), \( t \in A \) is in normal form if there is exists no other term \( s \in A \) such that \( t \rarr s \).
$$ \begin{align*} t \text{ is in normal form} &\iff \nexists s \in A \text{ such that } t \rarr s \\ \end{align*} $$
Strong Normalization#
A term is said to be strongly normalizing (SN) if all possible rewrites eventually reach a normal form and terminate in a finite number of steps. An ARS is strongly normalizing if all terms in the system are strongly normalizing (terminating).1326
$$ \begin{align*} & t \text{ is strongly normalizing} \iff \bold{\forall} s \in A \\ & \text{ such that } t \rarr^* s \text{, } s \text{ is in normal form} \\ \end{align*} $$
Consider the following ARS:
$$ \begin{align*} a &\rarr c \\ b &\rarr c \\ c &\rarr d \\ c &\rarr e \\ d &\rarr f \\ e &\rarr f \\ d &\rarr g \\ f &\rarr h \\ \end{align*} $$
The normal forms of this system are \( h \) and \( g \). Visualizing the relations above, we can see that any term can be rewritten to either \( h \) or \( g \) in a finite number of steps, making the system strongly normalizing.
Weak Normalization#
A term is said to be weakly normalizing (WN) if any rewrites reach a normal form and terminates in a finite number of steps.
$$ \begin{align*} & t \text{ is weakly normalizing} \iff \bold{\exists} s \in A \\ & \text{ such that } t \rarr^* s \text{ and } s \text{ is in normal form} \\ \end{align*} $$
To illustrate the distinction between strong and weak normalization (WN), consider the following ARS:
$$ \begin{align*} A &\rarr B \\ A &\rarr (AA) \\ \end{align*} $$
The term \(A\) is weakly normalizing because it can be rewritten to \(B\), a normal form. However, it’s not strongly normalizing since an infinite sequence of expansions can occur (see below). This highlights that while weak normalization ensures that a result can be found, strong normalization guarantees that the process of finding that result is always finite.
Conclusion Normalization#
Normal forms are important because they provide a unique term used to compare for equivalence12 and to prove properties of the system. In some systems, not all terms have a normal form, and the system is said to be non-terminating222326 and is the reason some rewriting systems are non-deterministic and undecidable.1
Conclusion#
Today we have explored the basics of rewriting systems, including the fundamental concepts, notation, and properties. We have seen how rewriting systems are used as a fundamental model for computational processes and reasoning in computer science, mathematics, and logic. They consist of a set of elements, terms, and rewrite rules that describe how terms can be transformed. Rewriting systems are used in many areas, including programming languages, compilers, and automated theorem proving.
I hope this article has helped you understand the basics of rewriting systems and that you have learned something new.
“Rewriting Systems”, https://en.wikipedia.org/wiki/Rewriting. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
“Term Rewriting and All That” by Franz Baader and Tobias Nipkow. Find the book on Cambridge Core or Cambridge University Press. ↩︎ ↩︎ ↩︎
“Abstract Rewriting System”, https://en.wikipedia.org/wiki/Abstract_rewriting_system. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Enno Ohlebusch, “Abstract Reduction Systems,” in Advanced Topics in Term Rewriting, ed. Enno Ohlebusch (New York, NY: Springer, 2002), 7–35, https://doi.org/10.1007/978-1-4757-3661-8_2. ↩︎
“Logic”, https://en.wikipedia.org/wiki/Logic. ↩︎ ↩︎ ↩︎
“Lambda calculus”, https://en.wikipedia.org/wiki/Lambda_calculus. ↩︎
“Term (logic)”, https://en.wikipedia.org/wiki/Term_(logic). ↩︎ ↩︎
“Binary relation”, https://en.wikipedia.org/wiki/Binary_relation. ↩︎ ↩︎ ↩︎
“Ground and Linear Terms”, https://en.wikipedia.org/wiki/Term_(logic)#Ground_and_linear_terms. ↩︎
“Boolean algebra”, https://en.wikipedia.org/wiki/Boolean_algebra. ↩︎ ↩︎
“Propositional variable”, https://en.wikipedia.org/wiki/Propositional_variable. ↩︎
“Equivalence (logic), https://en.wikipedia.org/wiki/Logical_equivalence. ↩︎ ↩︎ ↩︎
“Normal form”, https://en.wikipedia.org/wiki/Normal_form_(abstract_rewriting). ↩︎ ↩︎ ↩︎ ↩︎
“Conjunctive normal form”, https://en.wikipedia.org/wiki/Conjunctive_normal_form. ↩︎
“Closure (mathematics)”, https://en.wikipedia.org/wiki/Closure_(mathematics). ↩︎ ↩︎ ↩︎
“Transitive relation”, https://en.wikipedia.org/wiki/Transitive_relation. ↩︎ ↩︎ ↩︎
“Transitive closure”, https://en.wikipedia.org/wiki/Transitive_closure. ↩︎ ↩︎ ↩︎
“Reflexive relation”, https://en.wikipedia.org/wiki/Reflexive_relation. ↩︎ ↩︎
“Reflective closure”, https://en.wikipedia.org/wiki/Reflexive_closure. ↩︎ ↩︎
“Symmetric closure”, https://en.wikipedia.org/wiki/Symmetric_closure. ↩︎
“Equivalence relation”, https://en.wikipedia.org/wiki/Equivalence_relation. ↩︎ ↩︎
Aart Middeldorp and Hans Zantema, “Simple Termination of Rewrite Systems,” Theoretical Computer Science 175, no. 1 (March 1997): 127–58, https://doi.org/10.1016/S0304-3975(96)00172-7. ↩︎ ↩︎
Nachum Dershowitz, “Termination of Rewriting,” Journal of Symbolic Computation 3, no. 1–2 (February 1987): 69–115, https://doi.org/10.1016/S0747-7171(87)80022-6. ↩︎ ↩︎
“Confluence”, https://en.wikipedia.org/wiki/Confluence_(abstract_rewriting). ↩︎ ↩︎ ↩︎ ↩︎
“Completion (logic)”, https://en.wikipedia.org/wiki/Completeness_(logic). ↩︎
“Termination”, https://en.wikipedia.org/wiki/Rewriting#Termination. ↩︎ ↩︎ ↩︎
